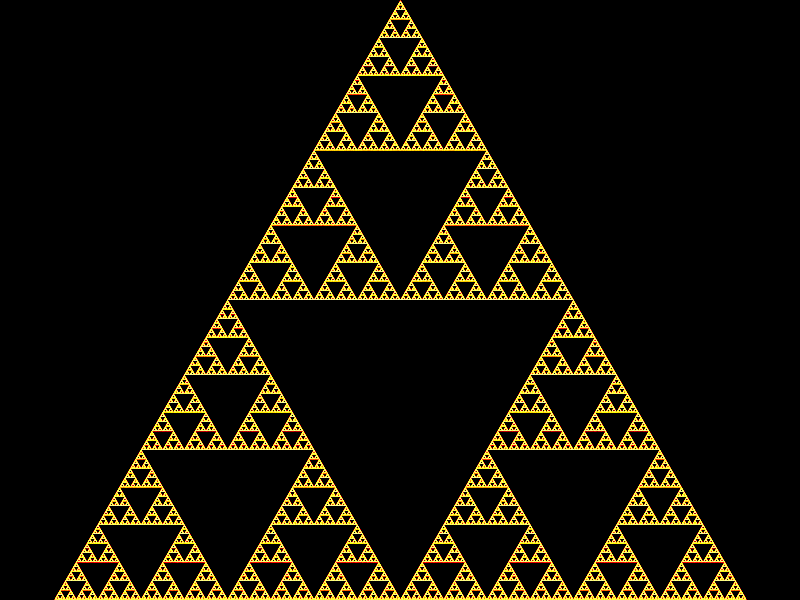While I was looking for pictures of soap bubbles spanning minimal surfaces for yesterday's post, I came across a cool site about wooden sculptures of minimal surfaces.
Archive for the ‘maths’ Category
Minimal surfaces
Friday, February 17th, 2006Overreactions to terrorism
Wednesday, September 14th, 2005I do not understand why a terrorist exploding a bomb which kills (say) 50 people is considered so much worse of a crime than (say) a serial killer murdering 50 random people for non-terrorist reasons. The objection people have to terrorism is, after all, the killing rather than the motive. If Al Qaeda pursued non-violent means to their ends instead of violent ones, they would not be nearly the enemy of the US that they are (in fact, their requests might even be taken seriously if they could persuade the US government to listen to them without violence).
I guess the point of taking terrorist crimes more seriously is prevention. Serial killers generally work alone, so once you have arrested one the stops. But if you arrest one terrorist (or he dies in the explosion he causes) there is always another to take his place. So in order to put an end to terrorism, the US government is attempting to eliminate all the people who could become terrorists, even if they have done nothing wrong. The trouble with that plan is that you have to turn this wonderful free country into a police state to do so. It is not enough just to arrest people who attempt to create or buy explosives or who contribute financially to terrorist causes, you also have to arrest people for the books they read, the photos they take, the websites they visit, the people they talk to and the things they say. You have to spy on everyone to find out if they have any sympathies for terrorist organizations. You have to completely gut the concepts of free speech and privacy which are some of the most important principles upon which the country is based. Already such rights are being eroded, and terrorism is showing no signs of disappearing. And instead of abandoning these dangerous and ineffective policies, the US government is trying to expand these anti-terrorist activities and erode more rights in the process. I think most people would (if they thought enough about it) rather take the freedoms we have along with a small chance of being killed in a terrorist attack than live in the world of 1984 but be safe from terrorists. As with all law enforcement it is a question of balance. I for one am more afraid of being arrested on suspicion of terrorism charges than I am of getting killed by a terrorist, which means that the balance has swung too far to the side of fascism. In fact I was in two minds whether to post this lest it be interpreted as supporting terrorism.
Here is what I think the government should do instead: treat terrorists as the criminals they are. There is no need to implement any special policies like deporting people to countries where they will be tortured, or imprisoning people indefinitely without trial, or removing judicial oversight from surveillance operations, or requiring libraries and bookshops to hand over their records. None of these things were needed in the past when it was just normal criminals that were being dealt with, so they should not be needed now. All that is needed is a sensible set of laws and the ability to enforce these laws. If we need laws against things like "possession of explosives with intent to murder" or "financially aiding a criminal organization" then so be it but no laws should be made limiting free speech or evading the checks and balances that have evolved to keep the system fair and just.
At the same time, the US government should be more open to considering the points of view of any political group who feels they have a legitmate gripe, even terrorist ones such as Al Qaeda (there is no point excluding the terrorist ones because any such organization will just split into two groups - a "political" one which does not officially endorse terrorism, but which secretly funds it, and a "military" one which blows things up). The idea is that if a group is given the same amount of attention whether or not they commit terrorism, there will be no incentive to commit terrorism. And there is still a definite incentive not to commit terrorism - namely that if you do so, your followers are liable to get arrested. Also, no-one should ever be left feeling that terrorism is the only option they have to get their point across.
And once you have your enemy sitting at the same table as you and prepared to talk, the war is half over.
Maths and music
Saturday, July 9th, 2005I love reading John Baez's column This week's finds in mathematical physics even though I usually only understand a tiny bit of it. This week he's talking about special relativity in 3 dimensions over the integers mod 7 - fascinating stuff, and a bizarre combination of physics and pure mathematics.
This morning I've been listening to this after having enjoyed listening to the single ("Emily") on the radio all week. I kept just missing the name of the artist because they would annouce it right before playing the song instead of right afterwards, but finally figured out what it was by googling some of the lyrics. Pretty good.
A new approach to the Monty Hall problem
Tuesday, August 24th, 2004Reams and reams have been written about the Monty Hall problem, but no-one seems to have mentioned a simple fact which, once realised, makes the whole thing seem intuitive.
The Monty Hall show is a (possibly fictional, I'm not sure) TV gameshow. One couple have beaten all the others to the final round with their incredible skill at answering questions on general knowledge and popular culture, and now have a chance to win a Brand New Car. There are three doors. The host explains that earlier, before the couple arrived, a producer on the show rolled a dice. If a 1 or a 4 was rolled, the car was placed behind the red door. If a 2 or a 5 was rolled, it was placed behind the blue door and if a 3 or a 6 was rolled, it was placed behind the yellow door.
The host invites the couple to pick which door they think the car is behind. He then opens one of the other two doors and there's no car behind the door! (He knows where the car is, so he can always arrange for this to happen). Then the host asks the couple if they want to change their mind about which door they think the car is behind. Should they change? Does it make a difference.
Most people's first reaction is that it can't matter. How can it? The car has a one in three chance of being behind each of the doors.
No-one would argue that the car has anything but a probability of 1/3 of being in behind the door the couple picked (say it's the red door). But when the host opens the blue door, magic happens. The probability of the car being behind the blue door suddenly goes to zero. The probability can't vanish (otherwise there would only be a 2/3 probability of there being a car at all) and it can't go to the red door so this ghostly 1/3 probability-of-there-being a car goes to the yellow door. The car now has a 2/3 probability of being behind the yellow door. "Poppycock!" most people would say. Probability isn't this "magic stuff" that can travel between doors. But the correct answer is that the couple should change doors - the car really does have a 2/3 probability of being behind the yellow door.
If you're in doubt, you could simulate the situation with a computer program, run it lots of time for the choices "never change doors" and "always change doors" and see what fraction of the time in each case the couple wins the car. You will find that changing makes you win 2/3 of the time, and sticking 1/3. Or you could enumerate the possibilities:
1/3: Couple picks correct door in the first place. If they change, they lose.
2/3: Couple picks the wrong door. The other wrong door is then eliminated, so if they change, they win.
So changing has a 2/3 probablity of winning. This reasoning sounds like a more plausible argument for changing doors.
The key to this matter, and what makes the whole thing confusing to those who don't realise this, is that probability depends on what you know. If you think about this for a while, it becomes obvious. A fair coin, when tossed, has a 50% probability of landing on heads. However, once the event has happened, the probablity collapses to 0% (if it landed tails up) or 100% (if it landed heads up). Let event A be the tossing of a coin at noon, and success defined by the coin landing heads up. At five seconds to noon the probability of success is 0.5. At five seconds past noon, when everybody can see that the coin landed heads up, the probability of success is 1.0. If the coin is tossed and it rolls under the sofa, then at five seconds past there is still a 50% chance of success. Although the coin has landed, no-one knows what the result is. Probability depends on what you know. If you know nothing about the coin, the probability of success is 0.5.
Suppose a neutral third party is the only one to see the coin, and says "I'm not going to tell you what it says, but I'm going to roll a dice (behind your back, so you can't see it). If it comes up even, I'll say "heads", whatever the coin says. If it comes up odd, I'll say what the coin says. But I won't tell you whether the dice came up odd or even." Suppose this third party then tells says "heads". There's a 50% chance that this was because he rolled an even number and a 50% chance that that's what the coin really said. What is the probability of success now? Well, we can enumerate the possibilities again and notice that of the four equally likely possibilities (Heads+even, Heads+odd, Tails+even, Tails+odd) the only one we've eliminated is Tails+odd, since in that case he would have said "tails". Of the remaining three possibilities (which are still equally likely), two of them involve success so the probability of success is 2/3. We can check this as follows: He says "heads" three out of four times, so the probability of success is (2/3)*(3/4)+0*(1/4)=2/4=1/2 (since we know there is 0 probability of success if he says "tails"). This is the answer we expected.
We conclude that, by cleverness, we can do a "partial collapse" of the probability by finding out a bit of information (if not all of it). In this case the knowledge that the neutral third party said "heads" doesn't give as much information about the state of the coin as seeing the coin itself - it doesn't tell us for definite whether we have heads or not, but it does impart enough information to change the probability.
This is exactly what happens in the Monty Hall problem. The host imparts some information to the couple about which door the car is behind, but not enough to tell for the couple to tell for definite which door the car is behind - just enough to shift the probability in favour of the door which they would choose if they opted to "change". If it was a complete probability collapse (i.e. if he opened any two doors) no-one would be in any doubt as to whether they should change or not. It's just because the probability has only partially collapsed that people get confused.
Addendum
Justin sent me this email:
I read your paper on "Monte Hall Strikes Back." and absorbed that probability depends on what you know. Following is the question that I made up and is having trouble "partial collapsing" it. Maybe you can help me out with an insight:
There are two doors, door #1 and door #2 behind which two real numbers are written at random. You get a prize if you choose the door with larger real number. At this point, the probability of winning a prize is 1/2. However, you get a chance. You first choose a door, and Monty shows you the number behind that door. What should you do in order to do better than 1/2? Or is it even possible to do better than 1/2?
The answer to the question hinges on how these two real numbers are chosen. If all real numbers are equally likely, you can never do better than 1/2 because for any real number x the size of the set of real numbers smaller than x is exactly the same size as the set of real numbers larger than x (this is easy to prove, just pair them up: for all y>0, pair up x-y with x+y).
Of course, the game can't work like that in the real world because most of the real numbers are extremely large (either positive or negative) and require more atoms than there are in the universe to write down.
Suppose we have a more reasonable probability distribution for ,
P(win; F(x)<\frac{1}{2}) = 1-F(x)[/latex]
[latex]\displaystyle P(win) = \int_{-\infty}^zf(x)(1-F(x))dx+\int_z^\infty f(x)F(x)dx[/latex] where [latex]F(z) = \frac{1}{2}[/latex]. Integrating by parts gives [latex]P(win) = \frac{3}{4}[/latex].
However, the probability of winning using the optimal strategy after you know x depends on the distribution and on the value of x, but can be anywhere between 1/2 and 1.
Addendum 2
John de Pillis, a Professor of Mathematics at University of California in Riverside, emailed me to let me know about a graphical "proof" that switching doors (or cups in this case) improves your chances of success. If you're still confused, his diagram might help.
This diagram appears in John's book "777 Mathematical Conversation Starters", published by the Mathematical Association of America.
Incidents & puzzles
Monday, March 22nd, 2004If you liked watching "airline" you'll love this: NASA Aviation Safety Reporting System incident reports. Fascinating stuff. Their monthly safety bulletin, Callback is also great reading (and more readable).
This weekend was the 7th quasi-annual Microsoft Puzzlehunt weekend. This time the theme was Lewis Caroll's "Alice" books. Our team ("The Badgers' Parade") came 36th out of 51. Not bad, but not as good as we had hoped. However, we did score a couple of good coups: we were the first team to solve a puzzle, and there were 3 puzzles that we were the first to solve (only the top 4 teams equalled or bettered that). I was pretty exhausted by the end - I only got 4 hours of sleep on Saturday night, and that was on a sofa in the atrium of building 18.
Economics for bluffers
Thursday, February 19th, 2004I'm off to England tomorrow. For the weekend. To get another Master's degree. It's going to be pretty hectic - it'll be a miracle if it all goes according to plan.
Technical difficulties...
Wednesday, September 3rd, 2003Rats, my email is down. My hosting company (Ghoulnet) knows about it but doesn't have an ETA for fixing it. In the meantime, all my email is bouncing.
I feel like I'm a ship adrift at sea...
I've been attempting to do Net Riddle. I have got to stage 1.48 but nobody seems to have completed that one yet, so my chances of passing it are slim at best.
Romantic mathematical puzzles
Tuesday, November 6th, 2001Those who know me will tell you that I am an incurable romantic, and also that I have a soft spot for mathematical puzzles and games. Here are some mathematical odds and ends that I have found to be unusually romantic - see what you think. Follow the links on the titles for further information.
The Happy End Problem
The Happy End Problem is so named because two of the mathematicians who met whilst working on the problem, E. Klein and G. Szekeres, got married and lived happily ever.
Suppose you have g>=3 points on the plane, no three of which are collinear.
For some arrangements of the g points, you will be able to pick n of them to make a convex n-sided polygon. For example, for n=3 you will always be able to make a convex triangle because all triangles are convex and no 3 points are collinear.
For n=4, g=4 does not suffice because the four points could be arranged as the corners of a triangle and a fourth point inside the triangle - no convex quadrilateral can be obtained from these points, but g=5 does (see figure 1).
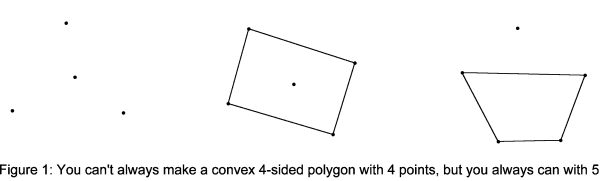
The problem is to determine the number of points g(n) you need to make an n-sided polygon no matter where the points are (as long no 3 of them are collinear).
The first few values of g(n) are:
g(3)=3
g(4)=5
g(5)=9
g(6)=17
Higher values are unknown, but at most the values of A052473:
g(7)<=128
g(8)<=464
g(9)<=1718
(Thanks to fjh for the correction.)
Mrs Miniver's Problem
According to Mrs Miniver, in the ideal romance each lover shares exactly two thirds of their interests with the other. She wishes to symbolize this with a diagram of two circles of the same size, overlapping such that the area of the overlap is that same as sum of the areas of each of the two crescents formed (half of the area of the overall figure). What is the ratio of the distance between the centres of the circles and their radii?
The answer is approximately 0.529864, and is believed to be trancendental.
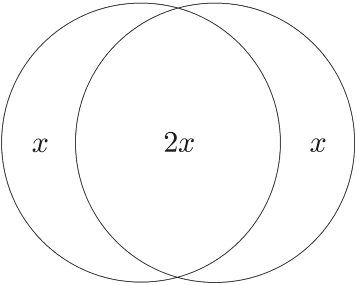
(An earlier version of the problem stated here was to find the answer if the intersection area was the same as the area of one of the crescents, which gives the answer 0.807946, but this isn't what Mrs Miniver originally stated as the ideal romance).
Happy numbers
Pick a positive integer n. Take the squares of the digits and add them up. Repeat. If you eventually get to 1, n is happy. If you don't, n is unhappy. The first few happy numbers in base 10 are 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100.
Friendly numbers
Two postive integers a and b are friendly if the sum of the proper factors of a is b and the sum of the proper factors of b is a.
Happy friendly numbers
Here's a romantic puzzle: in which bases (if any) can you find a pair of numbers which are friendly with each other and happy together?
The Kissing problem
An interesting article about kissing spheres.
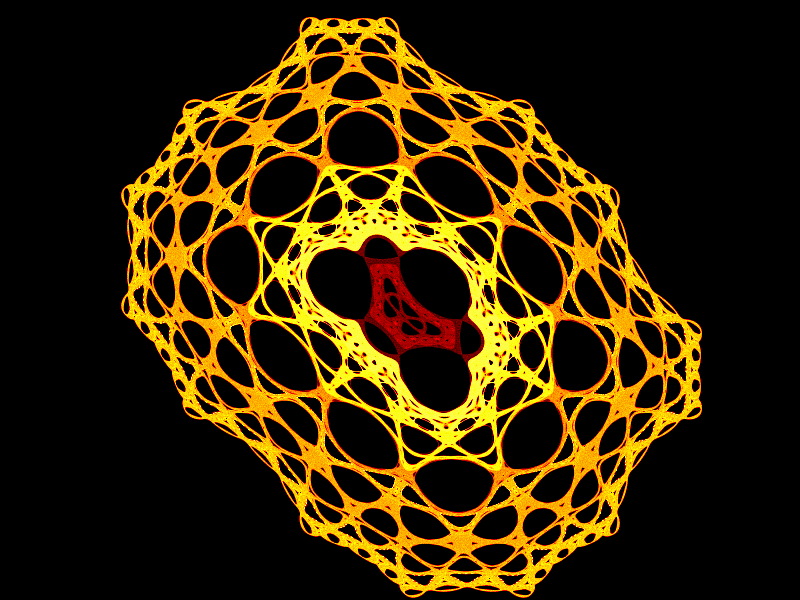
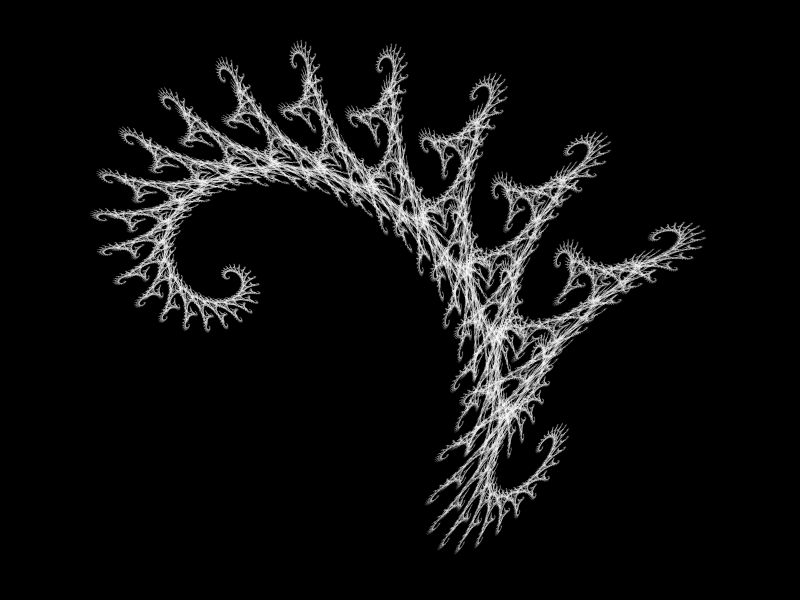
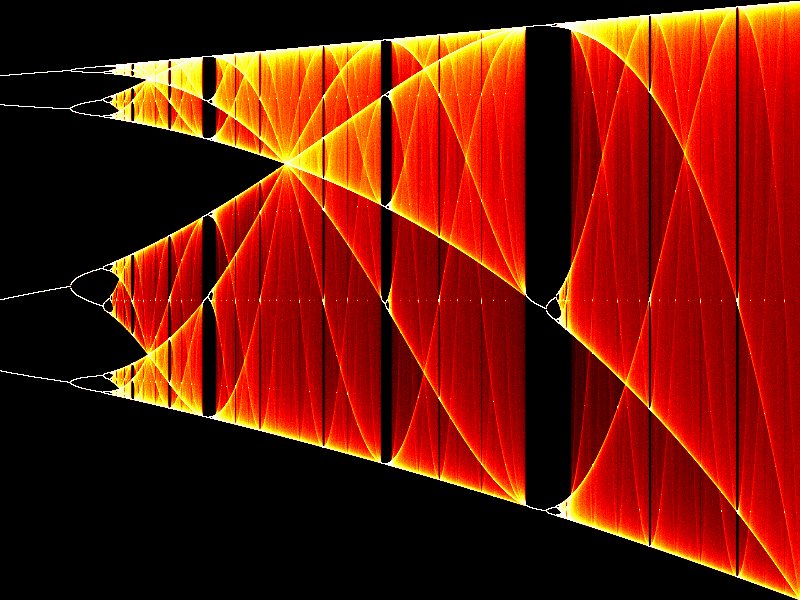
Fractal gallery
Friday, November 2nd, 2001Perfect numbers
Sunday, February 25th, 2001If you take any number and find all of its factors (including 1 but excluding the original number), then take the sum of all these factors, you will end up with another number. If this number is the same as the one you started with, it is a perfect number.
Perfect numbers are very rare. Only about 31 are known. The first few are:
- 6
- 28
- 496
- 8128
- 33550336
- 8589869056
Here are a few facts about perfect numbers:
- All perfect numbers end in either 6 or 8.
- If 2^n-1 is prime, then 2^(n-1)(2^n-1) is perfect. All perfect numbers are of this form.
- All perfect numbers are triangular.
- The digital root, or remainder when divided by 9, of any perfect number except 6 is 1.
- Every perfect number except 6 is the sum of consecutive odd cubes.
- The sum of the reciprocals of all the divisors of any perfect number is equal to 2.