Reenigne blog

Many years ago I wrote a ASCII/ANSI/text-mode design program called SCRDES (for screen designer). It was probably the most sophisticated thing I had ever written at the time - it had many features (circles, lines, rectangles etc.) and little text mode windows that would pop up over your drawing to do things like select different tools and colours and save or load your drawing. I mostly used it for designing levels for my game "Cool Dude".

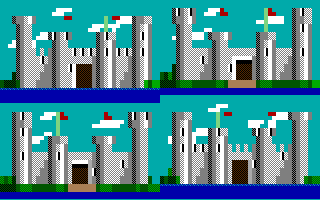
A bug in this program spawned an interesting little puzzle. The bug appeared right after I had added the user friendly interface with the text mode windows. These worked by saving the part of the screen behind the window and restoring it to make the window disappear again. However, the first time I tried to remove a window that was on top of a picture, I got some strange garbage instead of the picture I wanted. For example, the image:

would be turned into this:

Each time I created and destroyed the window, the garbage changed. I quickly realized that the bug was that I was saving the image into a string one way (scanning horizontally left to right and then top to bottom) and restoring it another way (scanning vertically top to bottom and then left to right). So I was putting back the same data, just in the wrong order.

The patterns in the garbage were interesting, so I wrote another program, called SPRITE (small bitmaps are often called sprites) which took an image and transformed it in this way repeatedly and which could be made to go forwards or backwards. I quickly discovered the following things:

• After a certain number of iterations in one direction, the picture becomes the same as the original. This number depends on the dimensions of the picture. A square picture, for example 8x8 or 25x25, would be restored to the original after only 2 iterations but anything more complicated takes many more. The 80x25 castle image above takes 999 iterations to return to the original.
• Some of the intermediate images consisted of smaller copies of the original arranged in a rectangular grid:

  

  Sometimes these smaller images would be upside-down, sideways, or even diagonal (straddling the edges in a toroidal fashion):

  

• Sometimes, instead of being shrunk, the image appears to be enlarged and interleaved with the other parts of itself:

  

After thinking about this for a while one can sort of see why it happens. Consider what happens to the point (1,0). After some number of iterations it will end up at the point (x,y) and the point (2,0) will end up at (2x,2y). The transformation is linear in some sense (modulo the edges) so you get affine transformations of the original image.

To figure out how many iterations it will take to return an x*y image back to its original self, I think one can just consider the trajectory of the point which starts off at (1,0) under the repeated applications of the transformation (a,b)->(⌊(bx+a)/y⌋,(bx+a) mod y) or, equivalently, the point 1 under the transformation c->(c mod y)*x+⌊c/y⌋ - once that ends up back where it started the rest will fall into place by linearity. I think the answer is the multiplicative order of x modulo xy-1, based on some tinkering with the OEIS, but I'm not sure how to go about proving it.

The trajectory can contain every point in the grid (except the top left and bottom right, which remain fixed) but does not necessarily do so. Some grids (for example 78x66) do but some only contain a fraction (<0.5) of the points. Of the 1998 remaining points in the 80x25 grid, for example, half of them are in the trajectory, the white ones in this image:

As you can see, this image is symmetrical under the transformation of rotating by 180° and switching black with white.

The following image was made by looking at all the of the possible grids from 2x2 to 65x65 inclusive, calculating the number of iterations required in each case, dividing by the number of points in the grid minus 2 and converting the resulting fraction into a shade of grey (white=1, black=0). So the white points correspond to grids that take the maximum number of iterations (xy-2), the next most common shade (mid-grey) corresponds to grids that take (xy-2)/2 iterations and so on.

I ran the program for grids up to 2001x2002 but the resulting image looks pretty homogeneous. White pixels seem to appear more often on lines corresponding to (some) prime numbers, but don't seem to get as rare as quickly as prime numbers do. Rational numbers <0.5 with small denominators seem to be show up more often.

Another open question is, given a x*y grid and a number of transformations n, how many castles will there be in the resulting image and what angles will they be at? (Or, dually, what fraction of a castle is magnified up to the entire sprite?).

Edit 14th July 2013:

This seems to be closely related (although not quite identical) to Arnold's cat map.

Reams and reams have been written about the Monty Hall problem, but no-one seems to have mentioned a simple fact which, once realised, makes the whole thing seem intuitive.

The Monty Hall show is a (possibly fictional, I'm not sure) TV gameshow. One couple have beaten all the others to the final round with their incredible skill at answering questions on general knowledge and popular culture, and now have a chance to win a Brand New Car. There are three doors. The host explains that earlier, before the couple arrived, a producer on the show rolled a dice. If a 1 or a 4 was rolled, the car was placed behind the red door. If a 2 or a 5 was rolled, it was placed behind the blue door and if a 3 or a 6 was rolled, it was placed behind the yellow door.

The host invites the couple to pick which door they think the car is behind. He then opens one of the other two doors and there's no car behind the door! (He knows where the car is, so he can always arrange for this to happen). Then the host asks the couple if they want to change their mind about which door they think the car is behind. Should they change? Does it make a difference.

Most people's first reaction is that it can't matter. How can it? The car has a one in three chance of being behind each of the doors.

No-one would argue that the car has anything but a probability of 1/3 of being in behind the door the couple picked (say it's the red door). But when the host opens the blue door, magic happens. The probability of the car being behind the blue door suddenly goes to zero. The probability can't vanish (otherwise there would only be a 2/3 probability of there being a car at all) and it can't go to the red door so this ghostly 1/3 probability-of-there-being a car goes to the yellow door. The car now has a 2/3 probability of being behind the yellow door. "Poppycock!" most people would say. Probability isn't this "magic stuff" that can travel between doors. But the correct answer is that the couple should change doors - the car really does have a 2/3 probability of being behind the yellow door.

If you're in doubt, you could simulate the situation with a computer program, run it lots of time for the choices "never change doors" and "always change doors" and see what fraction of the time in each case the couple wins the car. You will find that changing makes you win 2/3 of the time, and sticking 1/3. Or you could enumerate the possibilities:

1/3: Couple picks correct door in the first place. If they change, they lose.
2/3: Couple picks the wrong door. The other wrong door is then eliminated, so if they change, they win.

So changing has a 2/3 probablity of winning. This reasoning sounds like a more plausible argument for changing doors.

The key to this matter, and what makes the whole thing confusing to those who don't realise this, is that probability depends on what you know. If you think about this for a while, it becomes obvious. A fair coin, when tossed, has a 50% probability of landing on heads. However, once the event has happened, the probablity collapses to 0% (if it landed tails up) or 100% (if it landed heads up). Let event A be the tossing of a coin at noon, and success defined by the coin landing heads up. At five seconds to noon the probability of success is 0.5. At five seconds past noon, when everybody can see that the coin landed heads up, the probability of success is 1.0. If the coin is tossed and it rolls under the sofa, then at five seconds past there is still a 50% chance of success. Although the coin has landed, no-one knows what the result is. Probability depends on what you know. If you know nothing about the coin, the probability of success is 0.5.

Suppose a neutral third party is the only one to see the coin, and says "I'm not going to tell you what it says, but I'm going to roll a dice (behind your back, so you can't see it). If it comes up even, I'll say "heads", whatever the coin says. If it comes up odd, I'll say what the coin says. But I won't tell you whether the dice came up odd or even." Suppose this third party then tells says "heads". There's a 50% chance that this was because he rolled an even number and a 50% chance that that's what the coin really said. What is the probability of success now? Well, we can enumerate the possibilities again and notice that of the four equally likely possibilities (Heads+even, Heads+odd, Tails+even, Tails+odd) the only one we've eliminated is Tails+odd, since in that case he would have said "tails". Of the remaining three possibilities (which are still equally likely), two of them involve success so the probability of success is 2/3. We can check this as follows: He says "heads" three out of four times, so the probability of success is (2/3)*(3/4)+0*(1/4)=2/4=1/2 (since we know there is 0 probability of success if he says "tails"). This is the answer we expected.

We conclude that, by cleverness, we can do a "partial collapse" of the probability by finding out a bit of information (if not all of it). In this case the knowledge that the neutral third party said "heads" doesn't give as much information about the state of the coin as seeing the coin itself - it doesn't tell us for definite whether we have heads or not, but it does impart enough information to change the probability.

This is exactly what happens in the Monty Hall problem. The host imparts some information to the couple about which door the car is behind, but not enough to tell for the couple to tell for definite which door the car is behind - just enough to shift the probability in favour of the door which they would choose if they opted to "change". If it was a complete probability collapse (i.e. if he opened any two doors) no-one would be in any doubt as to whether they should change or not. It's just because the probability has only partially collapsed that people get confused.

Addendum

Justin sent me this email:

I read your paper on "Monte Hall Strikes Back." and absorbed that probability depends on what you know. Following is the question that I made up and is having trouble "partial collapsing" it. Maybe you can help me out with an insight:

There are two doors, door #1 and door #2 behind which two real numbers are written at random. You get a prize if you choose the door with larger real number. At this point, the probability of winning a prize is 1/2. However, you get a chance. You first choose a door, and Monty shows you the number behind that door. What should you do in order to do better than 1/2? Or is it even possible to do better than 1/2?

The answer to the question hinges on how these two real numbers are chosen. If all real numbers are equally likely, you can never do better than 1/2 because for any real number x the size of the set of real numbers smaller than x is exactly the same size as the set of real numbers larger than x (this is easy to prove, just pair them up: for all y>0, pair up x-y with x+y).

Of course, the game can't work like that in the real world because most of the real numbers are extremely large (either positive or negative) and require more atoms than there are in the universe to write down.

Suppose we have a more reasonable probability distribution for ,
P(win; F(x)<\frac{1}{2}) = 1-F(x)[/latex] [latex]\displaystyle P(win) = \int_{-\infty}^zf(x)(1-F(x))dx+\int_z^\infty f(x)F(x)dx[/latex] where [latex]F(z) = \frac{1}{2}[/latex]. Integrating by parts gives [latex]P(win) = \frac{3}{4}[/latex]. However, the probability of winning using the optimal strategy after you know x depends on the distribution and on the value of x, but can be anywhere between 1/2 and 1.

Addendum 2

John de Pillis, a Professor of Mathematics at University of California in Riverside, emailed me to let me know about a graphical "proof" that switching doors (or cups in this case) improves your chances of success. If you're still confused, his diagram might help.

This diagram appears in John's book "777 Mathematical Conversation Starters", published by the Mathematical Association of America.

Those who know me will tell you that I am an incurable romantic, and also that I have a soft spot for mathematical puzzles and games. Here are some mathematical odds and ends that I have found to be unusually romantic - see what you think. Follow the links on the titles for further information.

The Happy End Problem

The Happy End Problem is so named because two of the mathematicians who met whilst working on the problem, E. Klein and G. Szekeres, got married and lived happily ever.

Suppose you have g>=3 points on the plane, no three of which are collinear.

For some arrangements of the g points, you will be able to pick n of them to make a convex n-sided polygon. For example, for n=3 you will always be able to make a convex triangle because all triangles are convex and no 3 points are collinear.

For n=4, g=4 does not suffice because the four points could be arranged as the corners of a triangle and a fourth point inside the triangle - no convex quadrilateral can be obtained from these points, but g=5 does (see figure 1).

The problem is to determine the number of points g(n) you need to make an n-sided polygon no matter where the points are (as long no 3 of them are collinear).

The first few values of g(n) are:
g(3)=3
g(4)=5
g(5)=9
g(6)=17

Higher values are unknown, but at most the values of A052473:
g(7)<=128 g(8)<=464 g(9)<=1718 (Thanks to fjh for the correction.)

Mrs Miniver's Problem

According to Mrs Miniver, in the ideal romance each lover shares exactly two thirds of their interests with the other. She wishes to symbolize this with a diagram of two circles of the same size, overlapping such that the area of the overlap is that same as sum of the areas of each of the two crescents formed (half of the area of the overall figure). What is the ratio of the distance between the centres of the circles and their radii?

The answer is approximately 0.529864, and is believed to be trancendental.

(An earlier version of the problem stated here was to find the answer if the intersection area was the same as the area of one of the crescents, which gives the answer 0.807946, but this isn't what Mrs Miniver originally stated as the ideal romance).

Happy numbers

Pick a positive integer n. Take the squares of the digits and add them up. Repeat. If you eventually get to 1, n is happy. If you don't, n is unhappy. The first few happy numbers in base 10 are 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100.

Friendly numbers

Two postive integers a and b are friendly if the sum of the proper factors of a is b and the sum of the proper factors of b is a.

Happy friendly numbers

Here's a romantic puzzle: in which bases (if any) can you find a pair of numbers which are friendly with each other and happy together?

The Kissing problem

An interesting article about kissing spheres.

Note: This document is formatted as a text file using the IBM character set. To view it correctly, you should save this file and read it using a DOS editor such as EDIT, or change the current fixed-width typeface to a monospaced linedraw font, such as "MS Linedraw". Apologies if you don't have an IBM compatible computer or a monospaced linedraw font. If you don't have a linedraw font and your computer can understand Truetype fonts (most can these days), click here to download the MS Linedraw font.

I could reformat this using ASCII art or even GIFs, but it would take a long time and not be so pretty. Also, this would be impractical for the solutions.

PENTOMINOS Infrequently Asked Questions (iFAQ)
All the solutions to rectangular pentominos
10 by 6
12 by 5
15 by 4