It is impossible to travel faster than light, and certainly not desirable, as one's hat keeps blowing off. -- Woody Allen
Q1: Who is this page aimed at?
A1: It's aimed at people who are happy with the basic concepts of classical motion such as speed equals distance divided by time, but who know nothing about relativity (except maybe  and that you can't go faster than the speed of light) and wish to know/understand more.
and that you can't go faster than the speed of light) and wish to know/understand more.
Q2: What's the deal with relativity, then?
A2: Relativity was invented to account for a peculiar experimental result - that the speed of light is the same no matter how fast you are moving with respect to the source.
Q3: How do you do this experiment?
A3: Suppose you have an accurate timer, which is stopped when a pulse of light goes past it. Then you have another exactly the same. You bring them close together, synchronize them, and then move them slowly apart (Why slowly? You'll find out later). Now, fire a laser beam along the line connecting the two timers. By looking at the difference of the times recorded by the timers and dividing the distance between the two timers by this, you can measure the speed of light, which we'll call  for short from now on. (It's exactly 299,792,458 meters per second if you do the experiment in a perfect vacuum). Now, repeat the experiment but move the laser towards (or away from) the timers at speed
for short from now on. (It's exactly 299,792,458 meters per second if you do the experiment in a perfect vacuum). Now, repeat the experiment but move the laser towards (or away from) the timers at speed  whilst you're firing it. You'll notice that your estimate of the speed of light equals
whilst you're firing it. You'll notice that your estimate of the speed of light equals  , not
, not 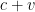 or
or  as you would expect if you know nothing about relativity.
as you would expect if you know nothing about relativity.
Q4: No, how do you really do this experiment?
A4: Unfortunately it's too difficult to do the experiment so directly in real life, so you have to do it more indirectly. For details, look up "The Michaelson-Morley Experiment" in any elementary textbook about special relativity.
Q5: Isn't this result because  is very large whilst
is very large whilst  is very small, so
is very small, so 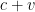 and
and  are roughly the same as
are roughly the same as  ?
?
A5: Nope, even if  is 99.9999% of
is 99.9999% of  , you'll still get the same result. The speed of light is an absolute constant (that's why it's called
, you'll still get the same result. The speed of light is an absolute constant (that's why it's called  for constant.)
for constant.)
Q6: What does this mean?
A6: It means that almost everything you thought you knew about space, time, speed and motion is wrong - they break down at high speeds (of the order of magnitude of  ).
).
Q7: Why can't you go faster than  ?
?
A7: The kinetic energy of a particle of mass 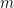 moving at speed
moving at speed  is not
is not  as they tell you in physics lessons in secondary school. The correct formula is
as they tell you in physics lessons in secondary school. The correct formula is 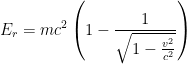 , which is approximately
, which is approximately 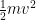 if
if  is much less than
is much less than  . Here is a graph of the classical kinetic energy
. Here is a graph of the classical kinetic energy 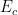 per unit mass and the relativistic kinetic energy
per unit mass and the relativistic kinetic energy  per unit mass, plotted against speed:
per unit mass, plotted against speed:
As you can see from this graph, as the velocity approaches  , the energy approaches infinity, so it requires an infinite amount of energy for any object with non-zero mass to even reach
, the energy approaches infinity, so it requires an infinite amount of energy for any object with non-zero mass to even reach  , let alone go faster. In fact, no information can travel faster than
, let alone go faster. In fact, no information can travel faster than  , even if that information carries no mass.
, even if that information carries no mass.

Q8: But light goes at  . How come?
. How come?
A8: Particles of light do not have any rest mass - the 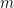 in the above equation equals zero.
in the above equation equals zero.
Q9: So light has no energy?
A9: No. Because it goes at  , you can't use the equation from question 7 to figure out the energy of a photon (a particle of light). The above equation gives zero times infinity, which is undefined. In fact, a photon can have any amount of energy, depending on it's wavelength or frequency. The energy of a photon
, you can't use the equation from question 7 to figure out the energy of a photon (a particle of light). The above equation gives zero times infinity, which is undefined. In fact, a photon can have any amount of energy, depending on it's wavelength or frequency. The energy of a photon 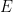 equals
equals 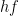 where
where  is the frequency (oscillations per second) and
is the frequency (oscillations per second) and 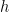 is Planck's constant (about 6.626x10-34 Joule-seconds).
is Planck's constant (about 6.626x10-34 Joule-seconds).
Q10: I've heard about "solar sails" - the idea that you can propel a spaceship using the momentum of light. But if the speed of light is finite and the mass of light is zero, then the momentum of light  . So how does the solar sail work?
. So how does the solar sail work?
A10: The equation for momentum 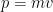 is another of those classical equations that are just plain wrong (well, not so much plain wrong as an approximation that only holds for velocities much less than
is another of those classical equations that are just plain wrong (well, not so much plain wrong as an approximation that only holds for velocities much less than  .) The correct equation is
.) The correct equation is  for particles with mass, or
for particles with mass, or  for photons.
for photons.
Q11: Okay, I'll accept for a moment that nothing can go faster than the speed of light. Suppose you're on a train that is moving at  with respect to the ground, and you're skateboarding down the aisle of the train on a jet propelled skateboard at
with respect to the ground, and you're skateboarding down the aisle of the train on a jet propelled skateboard at  . Now I'm going at
. Now I'm going at  with respect to the ground. What's the explanation of this apparent paradox?
with respect to the ground. What's the explanation of this apparent paradox?
A11: There is no paradox here. There's nothing in physics that says you can't have a train moving at  . According to relativity the laws of physics are the same in any reference frame so there's nothing special about
. According to relativity the laws of physics are the same in any reference frame so there's nothing special about  or any other speed (except
or any other speed (except  ) aboard the train. In fact, relativity says that you can't even tell how fast the train is moving by performing any experiment that doesn't rely on the outside of the train.
) aboard the train. In fact, relativity says that you can't even tell how fast the train is moving by performing any experiment that doesn't rely on the outside of the train.
The problem here is that if  is moving relative to
is moving relative to 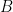 with speed
with speed  and if
and if 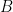 is moving relative to
is moving relative to 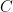 with speed
with speed 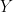 , the speed of
, the speed of  relative to
relative to 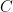 is not
is not  as you think it is. In fact, it is
as you think it is. In fact, it is 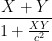 , which is always less than
, which is always less than  as long as
as long as  and
and  are, and this is approximately
are, and this is approximately  when
when  and
and 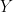 are much smaller than
are much smaller than  .
.
Q12: I heard about this thing called time dilation. What's that all about? And why did the timers have to be moved apart slowly in question 3?
A12: Suppose you have a set of twins. One of the twins stays on the Earth, the other goes on a round trip on a spaceship at a speed close to  . Because of the bizarre things that happen at speeds near
. Because of the bizarre things that happen at speeds near  , when the travelling twin returns, he will not have aged as much (will have experienced less time than) his brother who stayed on the Earth.
, when the travelling twin returns, he will not have aged as much (will have experienced less time than) his brother who stayed on the Earth.
Q13: But surely from the point of view of the twin on the spaceship, it was the earth which went on the relativistic round trip, and to him it should be the Earth-bound brother who should end up younger.
A13: No, the two brothers do not experience the same things. The one on the spaceship experienced an acceleration at the far point of its journey as he stopped moving away from the Earth and started moving back towards it. His reference frame was not "inertial" (did not move at a constant speed) so is not equivalent to the reference frame of his brother.
Q14: So just before the acceleration period, which brother is older?
A14: It may seem strange, but the question is not meaningful. You can't compare the ages of the brothers when they are a long distance apart. You can't compare times over a long distance and you can't compare distances over a long period of time. This is because relativistically, time and distance are two sides of the same coin. When moving at speed, time and distance "change places" to a certain extent - this is the source of time dilation and it's partner, length contraction.
Q15: Length contraction? What's that?
A15: When you're moving relative to something, say a plank of wood, that plank will be shorter (from your point of view) the faster you are moving relative to it, compared to the length it was when you weren't moving.
Q16: Suppose there's a 1 metre wide hole and a 2 metre wide plank. Suppose the plank is moving sufficiently fast that, from the point of view of the hole, the plank is length dilated to 1 metre. Then suppose that at the time the plank is passing over the hole, it goes through the hole. From the point of view of the plank, it's the hole that's length dilated (to 0.5m) so now the plank is too long to go through the hole. What's going on?
A16: The problem here is that the concept of rigidity is a classical one and has no equivalent in relativity. Think of the speed of sound - this is how fast mechanical signals travel through a material. In an ideal rigid body the speed of sound is infinite, but since no information can travel faster than  you cannot have a relativistic rigid body. So the simple answer to this question is that the the plank bends.
you cannot have a relativistic rigid body. So the simple answer to this question is that the the plank bends.
Q17: Hang on a sec. The plank bends in the reference frame of the plank, but not in the reference frame of the hole?
A17: Exactly. The fundamental thing here is the relativity of simultaneity. If two events happen simultaneously in one frame of reference, they do not necessarily happen simultaneously in another. This is why you cannot say what the difference in the age of the twins is when they are a long way away - the answer depends on your frame of reference.
Q18: What is the Cherenkov effect?
A18: Cherenkov radiation is a bluish light emitted when a particle moves faster than the speed of light.
Q19: WHAT!?!?!??!!!
A19: Notice that I said "speed of light", not  as I have mostly been using in the rest of this document.
as I have mostly been using in the rest of this document.  is the speed of light in a vacuum, the speed of light in materials is lower, and depends on the material. The speed of light isn't the absolute speed limit,
is the speed of light in a vacuum, the speed of light in materials is lower, and depends on the material. The speed of light isn't the absolute speed limit,  is.
is.
Q20: How do you actually do calculations with this stuff? It seems like all the starting points I've been taking for granted - space, time, velocity - aren't really fundamental any more.
A20: You can define a basis for space and time, however it will depend on your velocity, so you'll need a different basis for every reference frame you use. Fortunately, there is a simple formula for converting between reference frames, the Lorentz transform. You can read about this in any elementary special relativity textbook.
Q21: (From Gregg) If an object's mass increases as it's speed increases, where does this mass come from?
A21: From whatever accelerated the object. Mass and energy are the same thing. So when you increase the object's (kinetic) energy by speeding it up, you also increase it's mass. Now, energy can't be created or destroyed, so whatever gave the object this kinetic energy has lost some energy (and, therefore, mass) itself. Note that there isn't any transfer of matter going on in the acceleration process - the accelerated and accelerating objects have the same number of atoms (electrons, quarks...) in them that they started with, but the masses of these particles have changed.
Q22: (From Colin) Mass and energy are interchangeable. Has mankind managed to turn any energy into mass yet?
A22: Oh yes, physicists are doing this every day in particle accelerators. As the particles are accelerated they gain mass, then when they smash into each other they break up into many particles, some of which may well be the same particles that were originally accelerated. The particles that are "created" are effectively the result of turning energy into mass.
Q23: (From Colin) Mass attracts mass (gravity). Mass attracts energy (gravitational lensing etc). Has it been shown practically that energy attracts energy, or energy attracts mass?
A23: Not directly (in a lab) because the amounts of energy we can work with are too small to exert any gravitational attraction. The finest gravitational experients that have been done require masses of the order of a few grams, 1 gram of mass could power 80,000 homes for a year.
However, there are very good reasons to believe that energy does attract mass (and energy). Much of what makes up the "mass" in everyday substances is in fact energy (binding energy holding the protons and neutrons in the nuclei together). So if this energy didn't contribute to the gravitational force, we would expect that different substances (which have different ratios of mass to binding energy) would accelerate differently under gravity (because they would have different ratios of inertial mass to gravitational mass). Accurate experiments (to many significant figures) have been done measuring this ratio for many different substances, and no difference has been found between any of them. So if there is a difference in gravitational attraction between fermions ("matter" particles) and gauge bosons (the virtual "particles" responsible for "energies" of various sorts) it's very small (too small to be detected in any experiments anybody has devised so far).
Q24: (From Rachel) Something about Einstein's theory of relativity bothers me, specifically about the issue of time dilation. According to what I read (pls correct me if I'm wrong), the stronger the gravity the slower the pace of time. This was proven by experiments with clocks that seem to run faster when farther from the Earth, as well as with experiments wherein time delays for radio waves near a sufficiently dense body (such as the Sun) were observed.
Now, I understand that space distortions can be caused by sufficiently dense masses (similar to a rubber sheet weighed down in one part by a small yet heavy stone). But the reasoning regarding time doesn't convince me well. The experiments used to prove time dilation (as far as I know) had to make use of speed (i.e. a relationship between distance and time). This was the case for the experiments using clocks and radio waves.
So I wonder: What if... the apparent (take note: apparent) slowing down of time and the delays were caused, not by the true slowing down of time, but by the "stretching" of distances due to the presence of dense masses in space (much like the stone-on-rubber sheet again)? If so, then aging will occur at the same pace regardless of whether a person experiences high or low gravity.
Are there any experiments that disprove my assumption?
A24: The Pound-Rebka experiment verifies that time passes slower in a stronger gravitational field. By "makes use of speed" do you mean "assumes that the speed of light is the same no matter how strong gravity is"? I don't think any other speeds are involved. The constancy of the speed of light has been verified by other experiments.
Gravity bends space and it bends time, but it bends both in such a way that the speed of light remains constant (if only space were bent and time remained the same, the speed of light would have to change in proportion to the stretching of space).
The stone-on-rubber sheet image is a neat way to visualize matter bending space, but don't confuse the visualization with the physics - that model has some serious oversimplifications, especially where time is concerned.
If you have a question about relativity, email me (or comment below) and I might put it up here. I'm not going to do your homework for you, though.
If you think relativity is strange, just wait until you find out about quantum mechanics.
