Website for making websites

July 9th, 2010

This is an idea I came up with when I was working on Argulator. Making websites like this involves a lot of very fiddly work - keeping the server-side and client-side bits synchronized, implementing login/logout stuff and so on. It would be great if there was a site (a "MetaSite" if you will) that let you create data-driven web applications whilst writing a minimal amount of code - sort of like how WordPress lets you make a blog whilst writing a minimal amount of HTML and CSS.

MetaSite would have, built in, the ability to create user accounts, login, logout, change password and so on. The users thus created can then create their own sites and interact with sites built by others. Some sites might require email verification and/or a captcha solve before they will allow the user to do certain things - MetaSite would take responsibility for that and once these tasks are done they don't need to be redone for each application.

There would be an "admin hierarchy" in that an admin of a site can appoint other users as admins with special powers (moderation and so on) who can then further delegate their powers. Upon withdrawing power from an admin, that power is then withdrawn from the closure of admins they've delegated to.

Users would be given tools to allow them to specify which sites can access the information stored by which other sites. One such "built in" site might be a repository of personal information.

Another useful "built in" site would be messaging - a virtual inbox which sites can use to notify their users when events of interest happen.

Yet another useful "built in" would be a shopping cart application which lets applications act as online shops. So if you've written a site and you decide to add a feature which you want to charge users for, it's as simple as just ticking a box. Since payment is centralized with MetaSite, it would be possible to do micropayments (making a single credit card charge to buy "tokens" which can be spent on any MetaSite site).

So far, nothing too unusual - most of this has already been done. Where MetaSite really comes into its own is its rapid application development tools. If you want to create a blogging service, a photo hosting service, an Argulator clone, a wiki or whatever else, it's just a matter of defining what the "objects" that are stored in your system are and how users can interact with them. MetaSite would have various widgets built in so if you define one field to be a date and say that users can edit this date, all the code for a calendar control widget would be automatically instantiated. All the defaults would be secure, reasonably attractive and AJAXified so that the site is nice to use. When developers do need to resort to code it would be written in a sandboxed language (not just uploading raw PHP to the site, that would be a security nightmare). This language would have instrinsics which abstract out all the web-specific stuff and allow developers to just concentrate on their application domain.

This is the big difference between MetaSite and Facebook - if you want to create a Facebook application you need to have your own web server and you need to write the server-side code to run on it. MetaSite would have a very shallow learning curve - making a new site should be as easy as starting a blog.

Metasite applications would be limited in the amount of storage space and CPU time they can use, so that they don't adversely affect other sites. One way Metasite could make money would be to sell extra CPU time and storage space to sites that need it. MetaSite could also make it easy for site admins to add advertising to their sites to monetize them and/or pay for such extras. Another value added feature might be the ability to run a MetaSite site with a custom domain name, or even on your own server.

Everything on MetaSite would be customizable - objects, data editing widgets, even entire applications. In fact, the usual way of creating one of these would be to take an existing thing that's similar to the thing that you're trying to make, and modify it. These modifications could then be available to authors of other sites as starting points for their own things (in fact, I think this should be the default and the ability to keep your customizations proprietary should be a "value added" feature).

Ideally it would be the first stop for any web startup trying to get their site up and running as quickly as possible, but if nothing else it would be a way to take advantage of all those "I need a facebook clone and will pay up to $100" projects on vWorker (nee RentaCoder).

I've gone so far as to register MetaSite.org but I haven't done anything with it yet.

Posted in computer | No Comments »

VC++ inline assembly hack

July 8th, 2010

Here's a cute little hack I came up with when doing some fixed-point arithmetic stuff in Visual C++ a while ago. I wanted to make a templated C++ class with some inline assembly, the generation of which depends on a numeric template parameter. Doing the obvious thing doesn't work:

template<int N> class ArithmeticHelper<N>
{
public:
    static Int5 MultiplyShiftRight(Int5 x, Int5 y)
    {
        __asm {
            mov eax, x
            imul y
            shrd eax, edx, N
        }
    }
};

However, one can introduce numeric parameters into inline assembly code by pretending that they are the length of something, and using the "length" operator:

template<int N> class ArithmeticHelper<N>
{
private:
    static const int nn[N];  // VC's inline asm doesn't allow "shl eax, N" directly, but this works...
public:
    static Int5 MultiplyShiftRight(Int5 x, Int5 y)
    {
        __asm {
            mov eax, x
            imul y
            shrd eax, edx, length nn
        }
    }
};

Posted in computer | No Comments »

Most different colours

July 7th, 2010

For various visualization programming tasks, it's useful to have a set of colours that are as far apart as possible. I set out to write a program to generate such sets.

The first problem is that we must work in a perceptual colour space such as Lab rather than the usual sRGB, or our colours will be overly concentrated in the areas where sRGB over-represents.

Next, I set up a system of mutually repelling particles and let them arrange themselves (sliding along the sides and edges as required). This didn't work too well even just in sRGB space - the trouble is that I don't care about minimizing the distance to the most distant colours, only the nearest ones. I thought about do a Delaunay triangulation to find the nearest neighbours of each point, but it turns out that's overkill - all you need to do is just repel the 6 nearest particles (and recalculate what those particles are after each frame). If you end up with the closest points all on one side, the particle will be repelled away until one of the closest points is on the other side.

Even with this fix, I was still getting strange results. After some head-scratching, I realized that it was just to the "kinks" in the some of the edges of the sRGB gamut in Lab space:

The particles tend get "stuck" in these kinks.

I'm not quite sure what to do about this. Perhaps I can find optimal sets in a rectilinear gamut and then gradually morph this into sRGB while continuing to let the particles repel.

Posted in colour | 1 Comment »

Arbitrary precision Mandelbrot sets

July 6th, 2010

I added arbitrary precision arithmetic to my Mandelbrot zoomer. Surprisingly, the difficult part wasn't the arbitrary precision arithmetic itself, it was deciding when and how to switch from double-precision to arbitrary precision arithmetic. Because my program reuses data computed at one zoom level to speed up the computation of more deeply zoomed images, some images contained pixels computed using both methods. The trouble is, the two methods don't give the same results. In fact, after some experimentation I discovered that the problem was even worse than that: even using just the double-precision code, you get different results depending on the number of digits you use. So the point that was represented in my program by 0xffa615ce + 0x00000002i (using 10.22 bit fixed point) escaped after 548 iterations but the point 0xffa615ce00000000 + 0x0000000200000000i (using 10.54 bit fixed point) escaped after 384 iterations. The problem is that after every multiplication we shift the result right by the number of fractional bits, which performs a rounding operation. The images generated look reasonable but are actually only approximations to the true images that would be calculated if infinite precision were employed.

Having determined this, I realized it would be necessary to throw away all the points computed with lower precision once we started using a higher precision. This isn't as bad as it sounds, since (when zooming in by a factor of 2) the recycled points only account for 1/4 of the computed points but if we just threw them all out at once it would result in a visible artifact when passing through the precision boundary - the entire window would go black and we'd restart calculation from scratch. I wanted to avoid this if possible, so I started thinking about convoluted schemes involving restarting a point if its 3 sibling points were of higher precision. Then I realized that I could just recycle the points but keep their colours when splitting blocks to a new precision boundary, avoiding the glitch. There are still some artifacts while the image is being computed, but they are less jarring.

Finally there was the problem of interfacing with double-precision floating-point numbers. The Mandelbrot set is contained entirely within the circle |c|<2 and in this range a double has 52 bits of fractional precision. But if we replace the 10.22 and 10.54 bit fixed point numbers with doubles, we'll have a region of blockiness where we need 53 or 54 bits but only have 52. Rather than having two sorts of 64-bit precision numbers, I decided to simplify things and have 12 integer bits in my fixed point numbers. The program is very slow when it switches into arbitrary precision mode - it's barely optimized at all. The 96-bit precision code is currently has a theoretical maximum speed of about 92 times slower than the SSE double-precision code (190 million iterations per second vs 2 million). It could be significantly faster with some hand assembler tuning, though - I have a 96-bit squaring routine that should speed it up by an order of magnitude or so. All of the multiplications in the Mandelbrot inner loop can be replaced with squarings, since [latex]2xy = (x+y)^2 - x^2 - y^2[/latex]. Squaring is a bit faster than multiplication for arbitrary precision integers, since you only need to do [latex]\displaystyle \frac{n(n+1)}{2}[/latex] digit multiplications instead of [latex]n^2[/latex]. Given that we are calculating [latex]x^2[/latex] and [latex]y^2[/latex] anyway and the subtractions are very fast, this should be a win overall.

Posted in fractals | 2 Comments »

Waller's Torus: a four-dimensional musical instrument

July 5th, 2010

Consider the major and minor chords in Western music. There are 24 of them altogether (with the normal twelve-tone equal temperament tuning system usually used): one major chord and one minor chord for each of the 12 notes in the chromatic scale (A-G and 5 accidentals).

Each of these 24 chords consists of 3 notes. Pick one of the notes in the chord and throw it away, leaving two notes. Given these two notes, one can always find two chords (one major and one minor) which use those two notes. So given any major chord one can find three minor chords which share two notes with it, and given any minor chord one can find three major chords which share two notes with it.

That suggests that the 24 chords form a sort of network or graph, with vertices corresponding to chords and edges corresponding to pairs of notes. In three dimensions this network can be arranged on the surface of a torus (Waller's Torus). You can arrange the vertices in such a way that all the edges are the same length, but some vertices will have different sets of angles between edges than others.

In 4 dimensions, the symmetries of the network are more apparent - the vertices can be arranged such that each edge is the same length and all the vertices have the same set of angles between edges. The resulting object isn't a polychroron because only three edges meet at each vertex but it isn't a polyhedron either because it does extend into all 4 dimensions. The analogous figure in 3D would might be something like a star shape - if you draw it in 2D the inner points will be closer to each other than the outer points but in 3D you can arrange the points on the surface of a cylinder (sort of like the points one might find at the top of a paper party hat from a Christmas cracker). Here's what it looks like:

Using this figure, one could generate a nonlinear mapping from points in a 4-dimensional space to chords. Not just major and minor chords either - other chords are represented by points other than the vertices. At each vertex you can move in the direction of one of the edges to change the pitch of one of the notes. Since there are only three degrees of freedom in a chord (one for the pitch of each note) there is also a direction at each point in 4-space which leaves the chord unchanged as you move along it.

Posted in music | 3 Comments »

I am not (just) a strange loop

July 4th, 2010

A while back, I read Douglas Hofstadter's book "I am a strange loop". As one might expect from Hofstadter, it's a fascinating book packed with good ideas. However, it happens that I disagree with someone of them. Hofstadter believes that the human brain fundamentally works in an entirely mechanistic, deterministic manner and that all of the mysteries of consciousness can be explained in terms of symbols being triggered by other symbols in the brain. Our subjective "awareness" is, according to Hofstadter, just an illusion - a hallucination. I'm not convinced by this - the concept of a hallucination implies that there is something (someone) there to experience the hallucination. But if a hallucination has an experience, how can it be a hallucination? It's sort of like how the concept of "creating time" is meaningless, because the concept of creation implies a time before and a time after.

If "souls" (or whatever less loaded word you'd prefer to use to mean the part of us which has subjective experiences) are not made of particles or patterns of particles, how do they get distributed so that there's one per human brain? I think that's asking the wrong question, because it presupposes that souls are localized entities like particles. I think there are many other possibilities. Unfortunately because we have no way to do experiments on subjective experience, answering this question seems to be out of the reach of science (at least for the moment).

Posted in philosophy | 1 Comment »

Floating-point faster than integers

July 3rd, 2010

In an attempt to get a little extra speed in my fractal program, I decided to try rewriting the innermost loop to use 32-bit fixed-point numbers instead of double-precision floating-point numbers. The precision would be less good but I need to write some precision-switching code anyway. I had noticed that my CRT simulator got faster when I switched from floating-point to integer code, so I assumed (incorrectly, it turns out) that the same would be true in this program.

It turns out that the best way to multiply two signed 32-bit integers and then shift the 64-bit result right by 22 bits (the number of fractional bits I'm using) is to use the one-operand IMUL instruction followed by the SHRD instruction. Unfortunately the only register you get to pick with this combination is one of the input registers - both the output and the other input are in EAX. This is a problem because it means that you have to load EAX right before every multiplication and stash the result somewhere else right after, before starting the next multiplication. All this shuffling slows the code right down - my 2GHz Core Duo laptop peaks at ~150 million iterations per second for the double-precision routine and ~100 million iterations per second for the integer routine. To make matters worse, you also lose the use of the EDX register (which is stomped by the IMUL) so even with frame pointer omission you're down to just 5 registers (ESI, EDI, EBP, ECX and EBX).

Another possible way is to use the MMX registers and the PMULUDQ instruction, but that has two problems: the multiplication is unsigned and there's no arithmetic right-shift in the MMX/SSE ISA so it seems unlikely that it could be made faster than the IMUL version.

This makes me wonder if floating-point instructions would also be faster for other uses where integers have traditionally reigned supreme. Bignums for example. Instead of storing 32 bits of precision in each 32-bit register, you can store 52 bits of precision in the mantissa part of each 64-bit register. There is a little extra complexity involved since the floating point units aren't designed for this (and for multiplication you need to do four 26-bit*26-bit->52-bit multiplies instead of one 52-bit*52-bit->104-bit multiply). However, the extra bits might make this a win. Poking around at the gmp source suggests that they aren't currently using any such tricks for x86, though there is some FPU hackery on other architectures.

Posted in computer | No Comments »

Very low-level programming

July 2nd, 2010

In most computer programs where speed is critical, there are a small number of chunks of code in which the CPU spends most of its time - the innermost loops. For a fractal program, it will be the iteration function. For a high-precision number library, it will probably be the multiplication routine. For a video encoder, it might be the loop that searches for motion compensation vectors.

In each case, programmers will generally spend a lot of time optimizing these innermost loops for the most important CPU microarchitectures in order to squeeze out every last drop of performance where it really matters. This often involves hand-writing assembly code, modelling the execution pipelines of the target machine and poring over optimization documentation.

Doing this, programmers will often think things like "if only this CPU had an instruction that does X, which could be easily done in hardware, this routine could be so much faster". This is why every couple of years or so a new set of instructions is added to the x86 architecture: MMX, SSE, SSE2, SSE3, SSSE3, SSE4, AVX. These instructions are getting more and more complicated with time, which makes the optimization process all the more difficult - one might have to look at dozens of ways of doing something to find the best one for your specific task.

All this makes me wonder if there might be a better way. With each new instruction set extension, new functional units are added along with new ways of hooking them up. Suppose that instead of programming these inner loops the usual way (deciding which registers represent which variables, choosing instructions and ordering them) we could instead set some state inside the CPU that directly connected the output of multiplier 1 to an the input of adder 2 (for example) in effect creating a special purpose machine for the duration of the inner loop. The wiring up probably takes longer than running the original code would, but once you've wired it up each iteration through the loop can run extremely quickly, since there's no single execution thread causing a bottleneck. It would be essentially like having an FPGA built into your CPU.

I can think of several reasons why this isn't currently done. One is that writing applications at such a "low level" creates a dependency between the software and the most intimate details of the hardware. Tomorrow's CPU might be able to run today's software more quickly by having some extra multiplication units (for example) available to each core. But if the applications are addressing the multiplication units directly, that won't help unless the software is rewritten to take advantage of them. One possible answer to this might be to create a programming interface that involves a very large number of virtual functional units and allow the CPU to decide how to map that on to the actual hardware in the optimal way (possibly turning parts into more traditional code if it there aren't sufficient functional units) - a sort of "JIT Verilog" if you will.

A second reason is that when you increase the amount of state on the CPU affiliated with a particular execution thread, you make context switching more difficult, because there's more registers that need to get swapped out to memory. FPGAs are generally not reprogrammed extremely frequently because they contain a lot of state and it takes time to reprogram them. This could also be solved by virtualizing functional units, or it could be solved by keeping track of whether the CPU was reprogrammed since the last time the thread run, and only reprogramming when necessary. That would solve the common case at the expense of speed when doing dumb things like running two different video encoders at the same time (something that is also likely to be rather sub-optimal with todays CPUs, since it isn't generally something that is optimized for).

What would be even cleverer is if the CPU could examine the code sequence and wire things up automatically to maximize the speed of that inner loop. To some extent, CPUs are starting to do such things. Modern CPUs keep a queue of decoded instructions and if an inner loop fits into this instruction queue, no decoding needs to be done while it is running. Cache hints are another example of a transparent feature designed to allow optimization when specific hardware details are known.

Posted in computer | No Comments »

Random number generation on 8-bit AVR

July 1st, 2010

For my physical tone matrix I wanted a mode where at the start (or end) of each cycle the machine would pick a random "on" light and turn it off, and a random "off" light and turn it on. With 5-10 lights on, this makes a fairly nice little bit of random music - continually changing so it doesn't get too repetitive.

To implement this I decided the best way was to pick a frame (the second one of the cycle turned out to be the most convenient) and decrement one of two variables "randomOn" or "randomOff" depending on whether the current LED within the frame was on or off. If the variable reached zero the LED would be toggled. That doesn't take too many cycles. But the sample before this frame we need to generate random numbers and initialize randomOn and randomOff with them. randomOn needs to be in the range 0..lightsLit-1 (where lightsLit is the number of "on" LEDs) and randomOff needs to be in the range 0..(255-lightsLit). So we need to generate two random numbers in the range 0..n-1 where n is in the range 1..255 as quickly as possible. I wanted to try to generate these numbers in a single sample as trying to spread the work across multiple samples makes the program much more complicated. That left me with about 300 cycles to generate two random numbers.

The usual way of generating a random number in the range 0..n-1 is to generate a random number in a much larger range (say 0..65535) and use the modulo operation ("remainder after division by n") to get it into the range 0..n-1.

Generating a 16-bit random number is done in a fairly standard way using a Linear Congruential Generator (I used the X = 214013*X + 2531011 variant because it cuts out a few multiplications). That by itself takes nine 8-bit by 8-bit multiplications and 56 cycles. I rewrote it myself in assembly language rather than using the built-in generator from avr-libc, because the latter it not very optimized (it uses a full 32-bit multiplication which is not necessary).

If you use the 16-bit modulo function from libgcc it takes something like 215 cycles, which was too many. Even unrolled it's something like 144, which is still too many. I was about to embark on the work to spread this loop across several samples when I read this which describes a way of turning a division by a constant into a multiplication by a constant. That's not very useful for arbitrary division, since computing the multiplier constant is more work than just doing the division. But we're not doing arbitrary division here - we know something about our divisor n - it is no larger than 255. So it becomes practical to precalculate a table of multipliers and look up an entry in this table at runtime.

The next problem is that that method only works when the division is exact (has remainder zero) which is no good for this application since it's the remainder we're interested in. But the classic bit-twiddling reference book Hacker's Delight describes a variation which does work (for some divisors the dividend needs to be added back after the multiplication, and for some the result needs to be shifted right by a number of bits depending on the divisor). So our mod algorithm looks like this:

  1. Look up multiplier in table indexed by divisor
  2. Multiply dividend by multiplier
  3. Look up helper routine in table indexed by divisor (there are 18 variations - 9 possible shifts and either "add" or "don't add", but not all of them are used) and jump to it.
  4. Multiply by the divisor and subtract the result from the original dividend - the result is the remainder.

The resulting mod routine takes 40-53 cycles (depending on divisor) giving 96-109 cycles for the entire random number routine. With various other bits of overhead, the random routine takes 253 cycles on this "init" sample and up to 29 per sample on the first frame of the cycle.

Posted in algorithms | 2 Comments »

Physical tone matrix screen construction details

June 30th, 2010

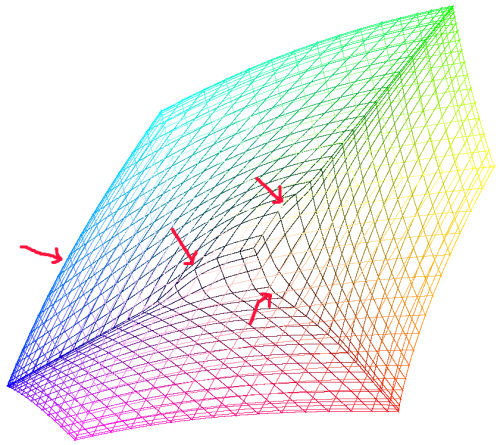
I think the most unusual thing about the physical tone matrix I posted about yesterday is the screen - I hadn't seen one like it before I made it, and having made one I now know why - they're very fiddly to make. I'd like to go into some more details about how it is made and how it works.

Step 1 is to cut out a 6" square piece of 1/8" thick acrylic. I bought a 12"x24" piece from Delvie's plastics (the cheapest shipped price I could find for such a small quantity), which is enough for 8 such screens (though I doubt I'll make another 7 since threading the wire takes so long - I hope I'll be able to make something else fun out of the rest, though). Cutting this stuff is really easy - just score it a few times with a knife and a straightedge where you want it to break, clamp it to a table so that the scored line runs along the edge of the table and then push down hard on the bit that protrudes over the edge of the table - it'll break cleanly along the scored line. Leave the backing paper on for now.

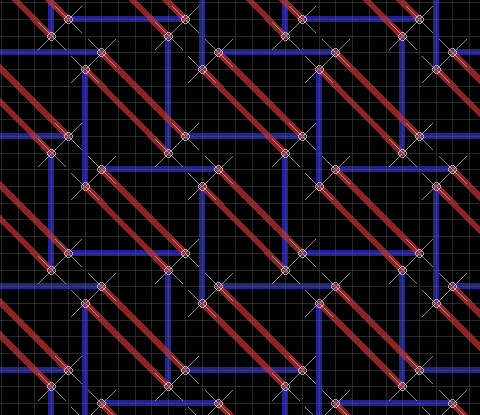
Step 2 is to drill the holes. I deliberated a bit about the hole pattern to use. I originally thought of threading the wires just horizontally and vertically, so that the switch was formed at the place where the two wires "cross over" (but don't quite touch) in the following picture (red is top, blue is bottom):

But then I decided I'd rather have the central point of the switch not have wire over it, so that the LED would be able to shine through at that point. I also realized that I'd be able to make the switches longer (and therefore easier to press) if the wires were arranged diagonally and fairly close to each other. Working backwards from where I wanted the wires to be on the top, I came up with this pattern:

This requires about 67 feet of wire altogether - because of the zig-zagging, each horizontal and vertical wire is about 15" on the matrix itself, with 2" spare on the top, left and right sides and 14" spare on the bottom to connect to the PCB. Use 22AWG solid-core hook-up wire - this should work nicely.

Here is a page showing where all the holes need to be drilled. Print this out and glue it on to one side of the acrylic sheet. Use a drill press to drill all 1,024 holes. I used this which is the cheapest one I could find. It's a bit flimsy but good enough for the purpose (as well as for PCBs, which is what it's meant for). It doesn't quite have enough clearance to reach the center holes if you put it together in the obvious way, but it does come with an attachment which lets you move the drill further away from the metal bar, if you jam a piece of plastic or something in the gap. I used these bits which seemed to work fine. The positioning doesn't have to be perfect but the closer the better. I think I used a number 68 drill bit or thereabouts - make sure your wire fits through the first hole you drill before drilling the rest. The plastic swarf from the drill will accumulate under the glued paper a bit but that doesn't really matter.

While you've got the drill press handy, make a hole of ~2mm diameter in each corner for the screws to hold it onto the PCB. The way I built it, the switch matrix is screwed to the PCB using 1-1/2" long screws and then the PCB is screwed to the bottom box, so the entire thing is rigid (the top of the box also screwed to the bottom of the box - only these screws need to be removed to change the batteries). Choose the positions of these holes carefully, since you will need to make holes in the same position in the PCB.

Step 3 is to remove the backing paper and sand the acrylic on the bottom side using a piece of sandpaper. Shine an LED through it to make sure it's diffusing properly. If you don't sand it the screen will have a very narrow viewing angle (depending on the LEDs used - cheap high brightness ones tend to have a very narrow viewing angle though) and when you can see them they will dazzle you. I think I used a #100 sandpaper or thereabouts - I don't think it matters much but try on a scrap piece first if you're worried. An orbital sander will probably get you a more homogeneous finish, but I just did it by hand (you can see the swirl patterns I made if you look at the screen very closely).

Step 4 is to cut and strip the wire. Cut 16 lengths of wire 19" long and 16 lengths of wire 31" long. Avoid kinking/bending the wire at this stage, to the extent you can. Use wire strippers to strip of all but 2" of insulation from the 19" lengths and all but 14" of insulation from the 31" lengths. You'll need to do this about 6" at a time. You might need to grip the 2" piece of insulation with pliers when stripping the last bit, otherwise you'll remove the wrong bit. Keep the pieces of insulation for step 6.

Step 5 is to thread the wire. Take each piece of wire in turn and thread it into the acrylic, starting at the bottom (31" sections) and the right (19" sections). Push the wire in so that the remaining insulation is right up against the bottom of the acrylic. Follow the pattern carefully - the top wire of each switch goes horizontally and the bottom goes vertically. Bear in mind that the pattern alternates each row, so if you start with the top one in the first row, you'll start with the bottom the second. The PCB has holes for soldering the top and left sides directly underneath the switch matrix, so make sure you pick the alternating pattern that gets it to line up. Make sure none of the wires touch each other - you can always pull them apart slightly with needlenose pliers if they do.

There is a bit of a knack to getting the wires flat and tight with no kinks. Here is how I did it. Suppose you have one segment threaded on the bottom and you're doing the next one on the top side.
a) Thread the loose end of the wire through the next hole. Pull it through. As you are doing so, make sure the wire is in the plane that is perpendicular to the acrylic sheet and that passes through the two holes. If the wire starts to twist over, adjust it so that it is back in this plane. If you don't do this, you'll get a kink in the wire when you pull it tight, which makes it difficult to get it to go where you want it to.
b) get a flat piece of metal (like the side of a pair of pliers) and push against the threaded segment on the bottom. This will prevent the bottom segment from being pushed up in the next step.
c) get another smaller flat piece of metal (like the end of another pair of pliers) and push against the newly threaded segment on the top. Start pushing at the "old" end (bending the wire into a right angle) and work your way along to the "new" end until it's totally flat against the acrylic sheet. If you don't do this there will be slack in the wire which will cause the switches to move when you touch them.

It gets more difficult once you get more of the wires in place, because you've got to navigate around the protruding ends with your flat edges. It might make it easier to do the outermost wires first and then work in towards the middle, but I didn't think that far ahead.

Once I got into practice, it took me about 20 minutes to do each wire, so about 11 hours of threading altogether (this is why I'm not planning to make any more). It's not too bad if you do a couple a day for a couple of weeks - one can carry on a conversation or watch TV at the same time.

Step 6 is to re-insulate the uninsulated loose ends. Cut 1" sections of insulation from the leftovers from step 4 and push them back onto the ends of the wire. If there are any bends or kinks in these parts of the wires you'll have to straighten them out with pliers first. Twist the insulation slightly as you push it back on and it'll go on more easily. This will help avoid short circuits when the circuit is partially assembled and you're testing it.

The switch matrix works by strobing each row and then testing each column. The rows are connected to the output of the "row" 74HC595 shift registers. They are connected via 10K resistors so that if something metal touches the switches they won't cause short out anything. The "active" row (which changes about 1,000 times per second) is brought to logic high (+5V), the others to logic low.

The switch columns are connected (again via 10K resistors) to 74HC4051 analogue multiplexers so that the microcontroller can specify (with three output bits) which of the 8 columns in each half of the matrix it wants to read. This column selection changes 15,625 times per second. The outputs of the two 4051s are connected to Darlington pairs which amplify the signal (which is very weak after it's passed through a finger) and pass it on to two input pins of the microcontroller (one for the left half, one for the right). Immediately after reading these pins, the microcontroller changes the multiplexer selection bits to maximize the time the circuit has to settle into the correct state for the next switch.

The Darlington pair bases are each connected to ground through a capacitor - they won't register as "on" until this capacitor charges up. The larger the capacitor the less sensitive the switches. If the capacitor is too small, you'll get "false on" readings from switches that you aren't actually touching (if the effect could be controlled this might make an interesting proximity sensor sort of input device but it's probably too finicky). If the capacitor is too large then you'll have to press the switches really hard or have damp fingers to for the touch to register.

Posted in hardware | 3 Comments »

« Older Entries
Newer Entries »